Gráficos
Los gráficos son claves a la hora de visualizar información. Algo a tener en cuenta es que al ver una curva en un gráfico, en realidad está compuesta por puntos unidos por rectas. Mientras la función sea continua las cosas van más o menos bien, pero al tener funciones con discontinuidades o asíntotas, podemos tener una visualización erronea.
Graficos de puntos
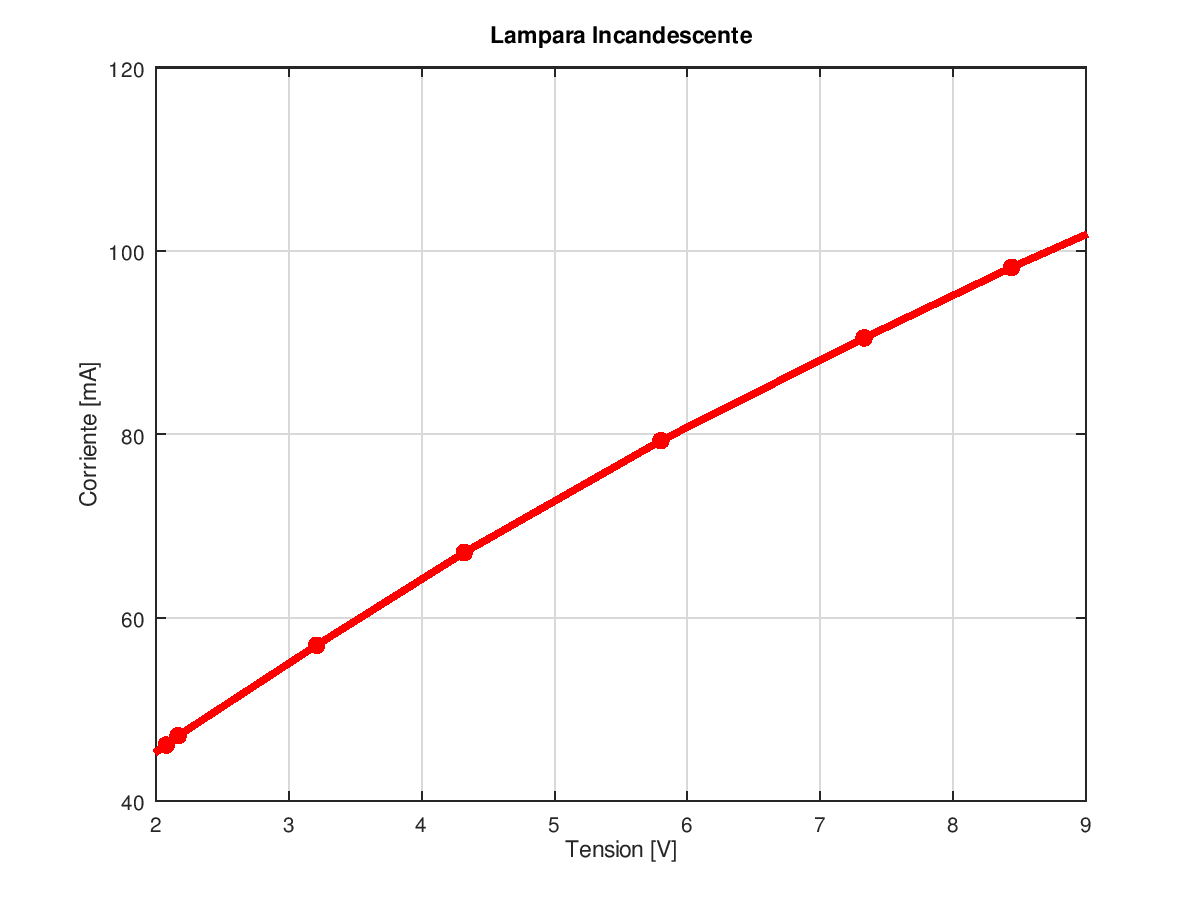
Los siguientes datos se corresponden a la tensión y la corriente en una lámpara incandescente, medidas con un voltímetro y amperímetro. Vamos a graficar para observar el comportamiento.
datos = [
#V[V], I[mA]
0.000 0.0
0.391 24.5
0.575 28.5
0.837 33.8
1.037 35.9
2.077 46.1
2.165 47.1
3.210 57.0
4.320 67.1
5.800 79.3
7.330 90.5
8.440 98.2
9.300 103.7
10.810 113.1
11.100 114.8
12.020 120.4 ];
V = datos(:,1);
I = datos(:,2);
Suele ser más claro escribir los datos como una matriz y de ser necesario, usar submatrices para obtener cada columna por separado.
Ahora que tenemos un vector con cada magnitud, podemos ejecutar:
plot(V,I)
La primera vez que se ejecuta plot puede taradar un rato, por alguna razón; luego de ese tiempo veremos una curva. Los puntos fueron unidos por rectas, lo cual se puede contemplar al hacer zoom.
Para observar los puntos, se le puede decir a octave:
plot(V,I, 'ro-')
El último parámetro indica tres cosas: El color del trazo, el tipo de puntos
y el tipo de recta usada para unir los puntos. Puede encontrar más información
ejecutando el comando help plot.
Para agregar más detalles, es necesario especificarlos uno por uno: primero el nombre de la propiedad y luego el valor:
plot(V,I, 'ro-', 'markersize', 5, 'linewidth', 3);
Decoraciones
Faltaría un título, nombres en los ejes, etc. Aquí va un ejemplo para analizar:
grid on; % Cuadrícula
xlabel("Tensión [V]");
ylabel("Corriente [mA]");
title("Lámpara Incandescente");
axis([2 9 40 120]); % [x_min x_max y_min y_max]
Gráficas de funciones
La forma de graficar funciones es como en la primaria, básicamente darle valores a “las x”, calcular el valor de “y” correspondiente, graficar los puntos “(x,y)” y unirlos con una línea.
Por ejemplo, vamos a graficar por este proceso:
x = [1 2 5 9];
y = 3*x+2;
# Muestro valores, no es necesario
disp(x);
disp(y);
plot(x,y);
Dado que es una recta, el gráfico es bueno. No ocurre lo mismo siempre:
x = [1 2 5 9];
y = 3*x.^3+2;
plot(x,y);
(Notar que usé el operador .^ en lugar de ^ ¿Por qué?)
La solución obvia sería poner puntos más juntos… pero es muy incómodo.
Para eso Octave tiene una función para crear N puntos equiespaciados,
basta con escribir x = linspace(inicio, fin, cantidad_puntos.
En este caso:
x = linspace(1,9, 1000); # Mil puntos entre 1 y 9
y = 3*x.^3+2;
plot(x,y);
También se podría haber usado un rango de la forma: x=1:0.01:9
o similar, pero muchas veces suele ser más comodo tener la cantidad
de puntos y no el paso.
Otros gráficos
El comando plot sirve para graficar puntos o curvas, pero tambien tenemos
otros comandos, muy similares para usar, por ejemplo:
semilogy()semilogx()loglog()stem()bar()polar()
Algunas de estas funciones tienen ciertas peculiaridades, pero las veremos más adelante si Dios quiere.