Introducción
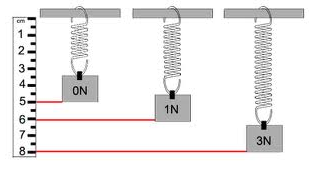
Tomemos de ejemplo el TP de Física I donde se mide la deformación de un resorte en función de la fuerza aplicada. Según la ley de Hooke, hay una relación lineal entre ambas variables.
Llamando a la fuerza aplicada en el resorte y el estiramiento, según la Ley de Hooke tenemos: (algunos ponen un - en esa ecuación, pero tomemos las referencias de forma de usar valores positivos, porque pintó).
Es medio complicado medir el estiramiento del resorte, por lo cual vamos a medir el largo sabiendo que . Por lo cual, podemos relacionar el largo y la fuerza según la ecuación:
$$L = 1/k F + L_0 $$
Dado que hay dos incógnitas ( y ) bastaría tener dos puntos para despejar el sistema. Por ejemplo, tomando los datos de la figura 1:
Tarea: Elegir dos de las ecuaciones y despejar y . Verificar que independientemente de las ecuaciones que se elijan, el resultado es el mismo.
Ajustando Valores
Al hacer mediciones en la vida real, siempre hay una incerteza de medición presente (y tal vez algún error sistemático, pero vamos a obviar eso). Podemos decir que cada medición xi que hagamos sobre una variable difiere levemente del valor verdadero, que llamaremos (que es el que queremos medir).
Podemos formular que , donde se comporta como una variable aleatoria con cierta distribución (generalmente normal de media nula, por cosas de la vida).
Si consideramos mediciones más realistas, es decir, teniendo en cuenta las incertezas de medición, es probable llegar a algo de la forma:
Si tratamos de despejar este sistema, resulta incompatible. Pero recordando
lo mencionado anteriormente, podemos escribirlo de la forma
y hacer A\b para obtener “la mejor solución”.
¿Estamos ajustando bien?
Alguien podría decir: En realidad el resorte no cumple con la ley de Hooke, y por eso el sistema es incompatible. ¿Cómo saber que el ajuste está bien?
Una forma de analizarlo es ver la distribución de probabilidad del error que
podemos calcular como err = b - A*xsol. Podemos obtener un histograma
haciendo hist(err), donde esperaríamos ver una especie de campana.
Por otro lado, el error de cada punto debe ser independiente del anterior.
Encontrar alguna tendencia en el error significa que seguramente hay algún
comportamiento que se nos está comparando. Para ello, basta hacer el producto
interno del error consigo mismo desplazandolo instante a instante.
Al hacer stem(xcorr(err)) esperaríamos ver una delta en el origen y
valores pequeños afuera.